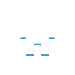第二百零一章:NS方程[2/2页]
天才一秒记住本站地址:[谷歌中文网]https://m.gugezw.com最快更新!无广告!
按捺不住心中的想法。
毕竟在多复变函数论与光滑流形领域这方面,他曾有着巨大的贡献,也深入了解这方面的知识。
1974年时,他证明了‘一个具有光滑边界的严格伪凸区域到另外一个的双全纯映射可以光滑地延拓到边界上这个世界难题。
这是20世纪许多数学家尝试证明都没有成功的。
因为多复变的区域和单复变情况不同,两个单连通区域不一定双全纯等价,这样单复变的方法不能够应用。
而他用自己独创的新方法解决了这个问题。
基于此,费弗曼曾经有数次向ns方程发起过冲锋的经历,但最终都以失败告终。
而徐川的到来,给他带了新的曙光,思虑了良久,他最终还是鼓起了勇气向徐川提议联手尝试解决的ns方程。
而对于费弗曼的提议,徐川没有任何犹豫直接就答应了。
纳维斯托克斯方程是他上辈子最想解决的问题之一。
解决它,或许就有希望遏制住可控核聚变中的超高温等离子体湍流这条恶龙,给它套上缰绳进行驯服。
为此,他上辈子选择了和费弗曼教授进行合作。
但遗憾的是受限于他的数学能力和费弗曼教授的物理能力,这种问题最终没有得到结果。
轮回一世,他再度来到了普林斯顿,再度和费弗曼展开了合作,而解决的对象依旧是ns方程。
这不由的让人感叹,命运的确奇妙。
.......
普林斯顿高等研究院。
徐川的办公室中,费弗曼正在一面黑板上用白色的粉笔写着。
“λ1(u)
第二百零一章:NS方程[2/2页]
『加入书签,方便阅读』
 大国院士
大国院士
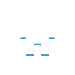
 大国院士
大国院士